学习线性分析法的起因是密码学课程的一次论文阅读的大作业,题目如下:
线性分析法
找了许多讲线性分析法的文章,但因为牵扯比较多的数学问题,所以大部分看起来都比较晦涩难懂,最后找到一个MOOC课程,讲的比较浅显易懂:
还找到了一个关于线性分析法的CTF题目zer0SPN:
从S盒说起
一切都得从S盒说起,S盒是一个代换表,输入X,根据代换表,输出Y,则:
- 已知S盒,已知X,可解出Y
- 已知S盒,已知Y,可解出X
但假如我只知道输入X(输出Y)的某几个比特,在已知S盒的前提下,我们有可能得到什么信息呢?
- 答:可能知道输出Y (输入X)的某几个比特间的概率关系!例如,考虑如下4进4出S盒:
| input | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| output | E | 4 | D | 1 | 2 | F | B | 8 | 3 | A | 6 | C | 5 | 9 | 0 | 7 |
把S盒按bit拆开:
| X1 | X2 | X3 | X4 | Y1 | Y2 | Y3 | Y4 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
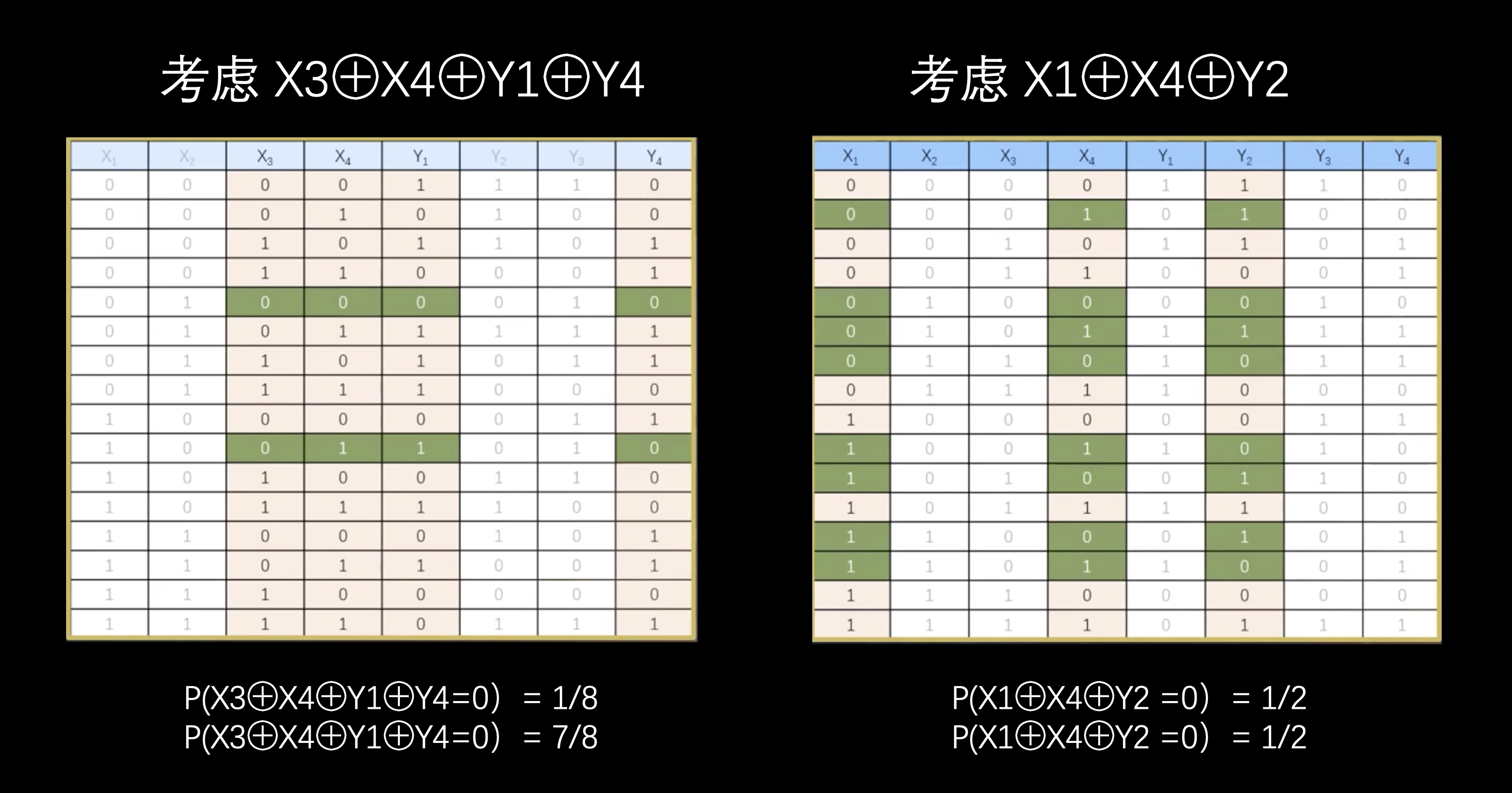
这种输入的某些比特和输出的某些比特异或的表达式,是一个只有0和1的异或表达式,结果也就是0和1两种情况,在没有任何信息可以利用时,输入是随机的,这个表达式等于0或1的概率应该均为1/2。
如果一个S盒设计有缺陷,则经过S盒变换后的输出和输入是有一定的概率关系的。所以,当知道输入X(输出Y )的某几个比特,在已知S盒的前提下,就可能知道输出Y(输入X)的某几个比特间的概率关系!但是单独一个S盒,看起来好像并没有什么卵用。
考虑SPN
考虑一个SPN((Substitution Permutation Network),如图:
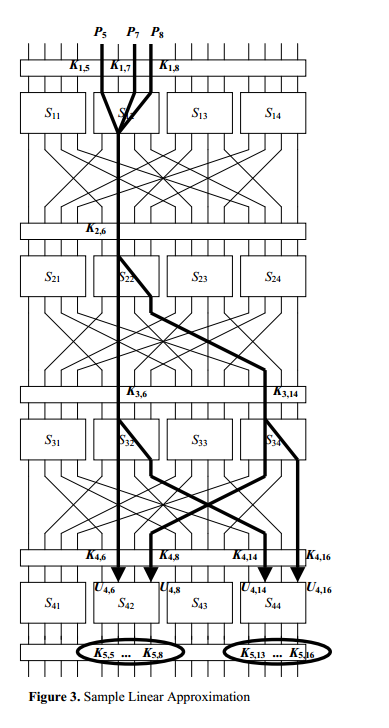
如果能寻找到类似如图的路径,使得路径上的比特位(明文比特,各个轮的秘钥比特,密文比特)所满足的约束(一个异或方程),是以大于0.5的概率成立的。那么我们便可以通过大量的明密文对(已知明文攻击),来计算出秘钥比特位的约束,从而减少秘钥空间,最终解出秘钥。这里给出华中科技大学MOOC中的关于线性分析法的定义:
线性密码分析,是通过分析S盒的线性特性,发现明文比特,密文比特和秘钥比特之间可能存在的概率线性关系,即存在一个比特子集使得其中元素异或表现出非随机的分布来进行密码分析的方法。
- 首先要找到,S盒的缺陷表达式
- 然后需要找到在改密码算法的迭代结构下,由于S盒这种缺陷引发的概率问题的传播方法。
- 再根据传播方法,找到一条路径,使得在全路径上的约束条件仍然能以一个较大于0.5的概率被满足。
- 根据大量的明密文对,不断的猜测秘钥的某些比特位,如果猜对了,则在该秘钥下,约束条件被大概率满足。
zer0SPN
题目:
- 给出了密码算法
- 65536对明密文对
- flag为初始秘钥
解法:
- 计算s盒缺陷表达式
- 计算全路径约束
- 利用明密文对,每次两字节,爆破最后一轮子秘钥
- 根据秘钥调度算法,反推初始秘钥
简单优化了一下S盒的缺陷表达式的函数,只要是进出bit相同的,直接就可以计算了:
sbox = [62, 117, 195, 179, 20, 210, 41, 66, 116, 178, 152, 143, 75, 105, 254, 1, 158, 95, 101, 175, 191, 166, 36, 24, 50, 39, 190, 120, 52, 242, 182, 185, 61, 225, 140, 38, 150, 80, 19, 109, 246, 252, 40, 13, 65, 236, 124, 186, 214, 86, 235, 100, 97, 49, 197, 154, 176, 199, 253, 69, 88, 112, 139, 77, 184, 45, 133, 104, 15, 54, 177, 244, 160, 169, 82, 148, 73, 30, 229, 35, 79, 137, 157, 180, 248, 163, 241, 231, 81, 94, 165, 9, 162, 233, 18, 85, 217, 84, 7, 55, 63, 171, 56, 118, 237, 132, 136, 22, 90, 221, 103, 161, 205, 11, 255, 14, 122, 47, 71, 201, 99, 220, 83, 74, 173, 76, 144, 16, 155, 126, 60, 96, 44, 234, 17, 215, 107, 138, 159, 183, 251, 3, 198, 0, 89, 170, 131, 151, 219, 29, 230, 32, 187, 125, 134, 64, 12, 202, 164, 247, 25, 223, 222, 119, 174, 67, 147, 146, 206, 51, 243, 53, 121, 239, 68, 130, 70, 203, 211, 111, 108, 113, 8, 106, 57, 240, 21, 93, 142, 238, 167, 5, 128, 72, 189, 192, 193, 92, 10, 204, 87, 145, 188, 172, 224, 226, 207, 27, 218, 48, 33, 28, 123, 6, 37, 59, 4, 102, 114, 91, 23, 209, 34, 42, 2, 196, 141, 208, 181, 245, 43, 78, 213, 216, 232, 46, 98, 26, 212, 58, 115, 194, 200, 129, 227, 249, 127, 149, 135, 228, 31, 153, 250, 156, 168, 110]
def find_sbox_vul(s):
import math
s_lenth = len(s)
s_bit = int(math.sqrt(s_lenth))
for insum in range(s_lenth):
for outsum in range(s_lenth):
if insum&(insum-1) and outsum&(outsum-1):
continue
bias = sum((bin(x&insum).count('1') + bin(s[x]&outsum).count('1')) % 2 for x in range(s_lenth)) - s_lenth/2
if abs(bias) > s_lenth/6:
print '+'.join(['X'+str(i) for i in range(s_bit) if insum&(2**i)] + ['Y'+str(i) for i in range(s_bit) if outsum&(2**i)])
find_sbox_vul(sbox)
为啥叫线性?
上课问了老师这个问题,为啥这种异或关系可以称之为线性?因为在我的理解中,形如y=ax+b的东西叫做线性。老师说一种运算满足加性和齐性就叫做线性。后来一个同学说,你们学的的不是同一个数学😹
在现代学术界中,线性关系一词存在2种不同的含义。其一,若某数学函数或数量关系的函数图形呈现为一条直线或线段,那么这种关系就是一种线性的关系。其二,在代数学和数学分析学中,如果一种运算同时满足特定的“加性”和“齐性”,则称这种运算是线性的。
出自维基百科:线性关系
但是为啥这种异或满足加性和齐性,我还是没明白,下次课继续问一下。
DES加密
拼接出一张DES加密的全景图,主要分为三个部分,Feistel迭代结构,轮函数,以及秘钥调度算法:
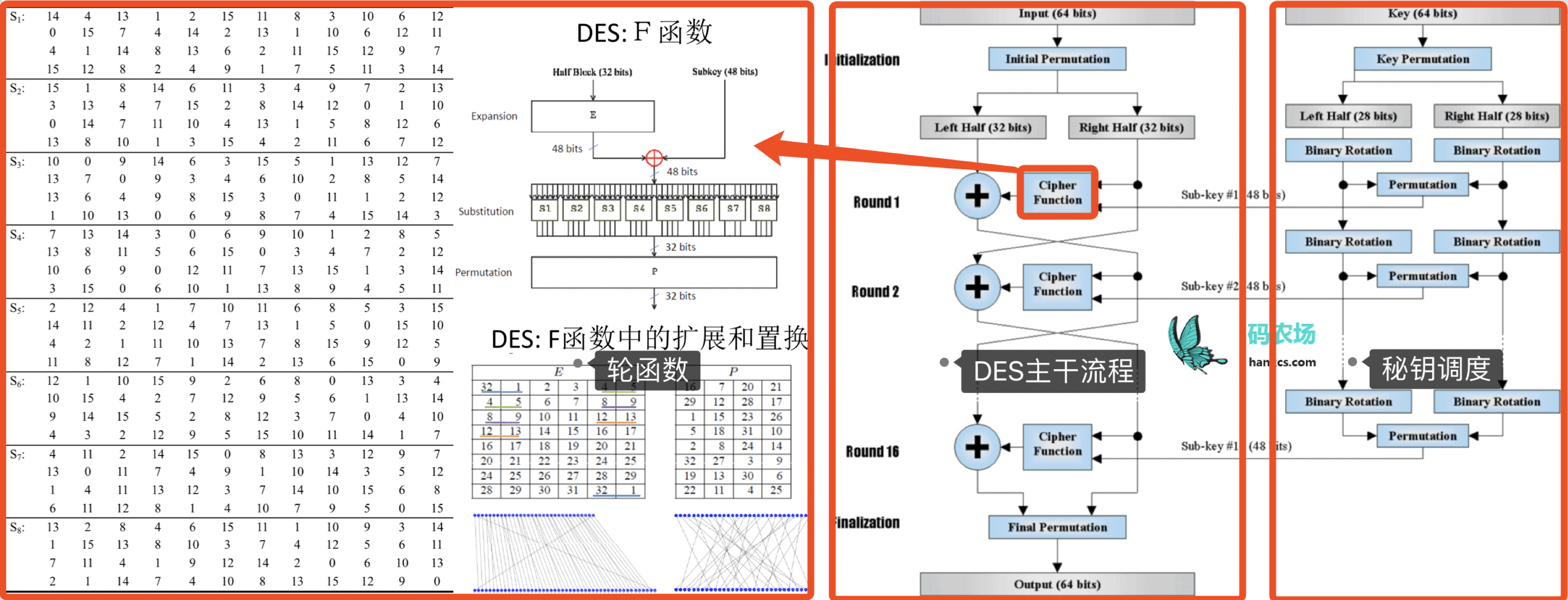
线性分析法分析DES
阅读文章:
参考如下文章:
原理还是从S盒出发,找到S盒的一些线性缺陷表达式,然后按照迭代结构推算:
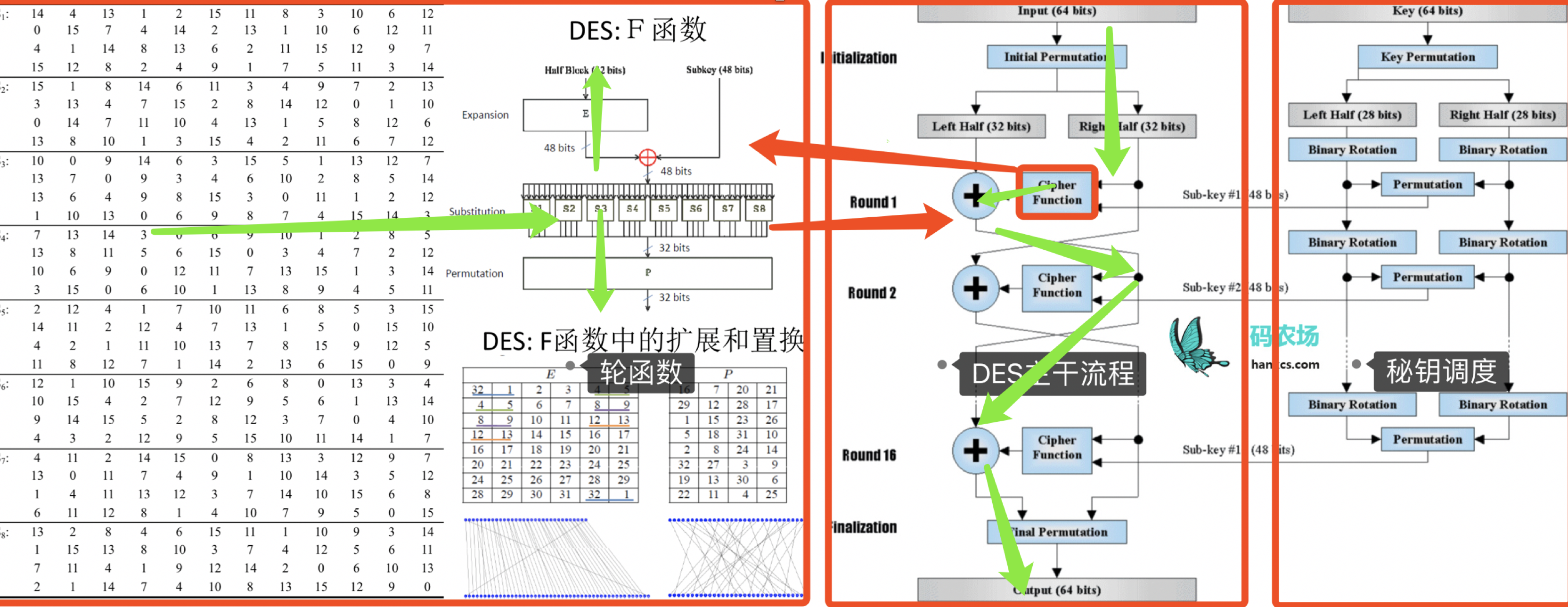
然后从S盒的缺陷表达式推到每一轮的输入输出和秘钥之间的关系:
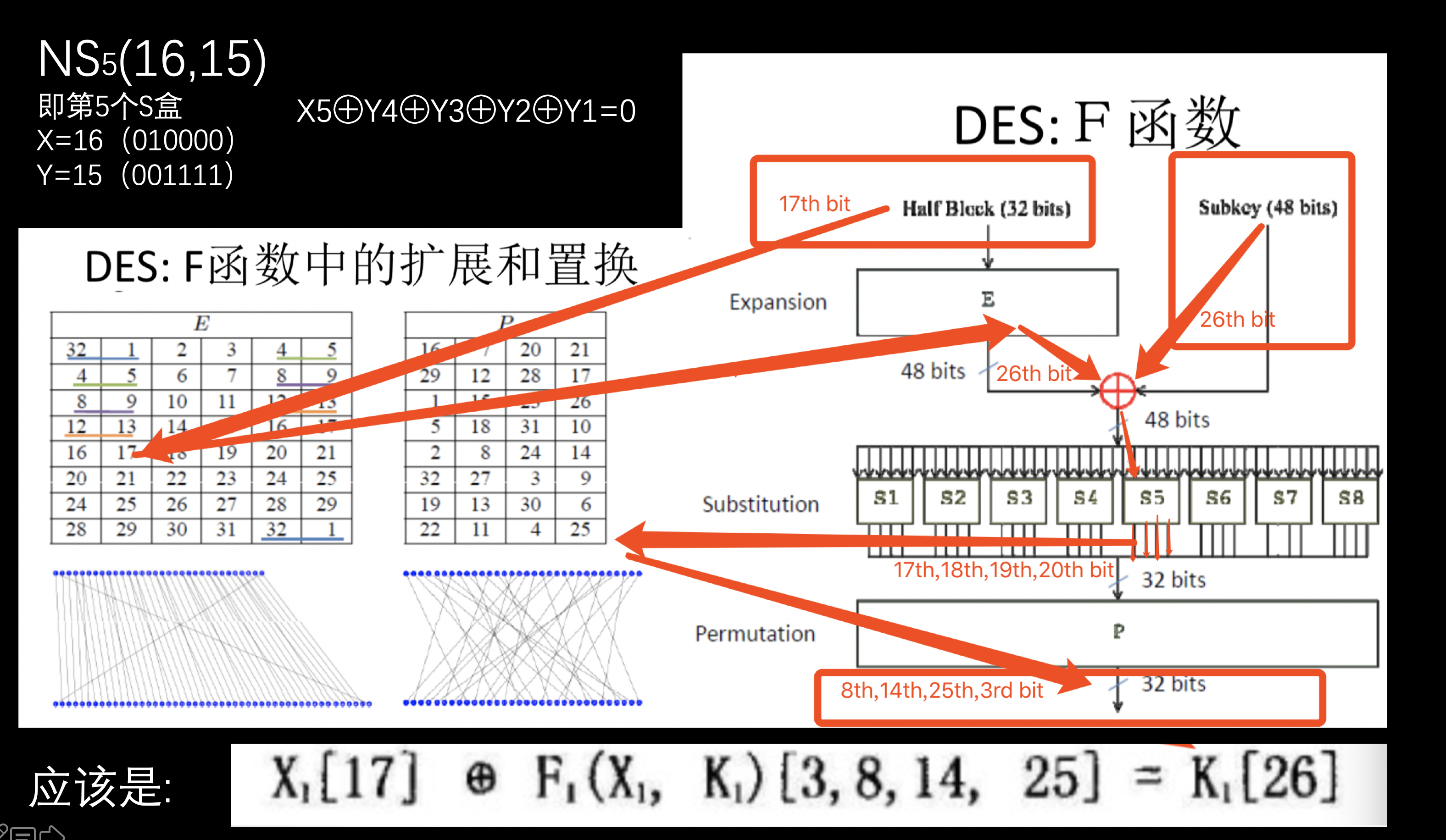
按照正常推演结果应该是:
X[17]⊕F(X,K)[3,8,14,25]=K[26]
但是文章中的结论却是:
X[15]⊕F(X,K)[7,18,24,29]=K[22]
但这里的结论是令我百思不得其解的,查找7,18,24,29怎么来,只能查到彩票,最后才在景运革的文章中找到跟我计算出是相同的结果。第二题上课老师提醒到,其实是日本人的计数方式不同:

在以上的4篇参考文章中,只有景运革的文章用比较正常的数制写出了推导关系。而那三篇信大的论文,非常暴力的翻译了93年的原文,并没有做任何解释,着实让我耽误了很久的时间。
最后推到R-1轮,然后爆破秘钥,和zer0SPN的思路相同:

总结
线性密码分析,本质是因为S盒设计存在缺陷,使得经过S盒的输入输出存在线性特性(异或方程)。通过分析S盒的线性特性(缺陷),结合密码算法的迭代结构,有可能发现整个密码算法中,明文bit,密文bit,秘钥bit三者之间存在的概率线性关系(异或方程)。则可根据大量的明密文对,对于秘钥bit进行相关分析,进而解出秘钥。故无论是SPN还是Feistel ,思路都差不多,主要是在路径的分析上有所不同,常规步骤如下:
- 计算s盒缺陷表达式
- 计算全路径可用约束
- 利用明密文对,爆破最后一轮子秘钥或者部分秘钥
- 根据秘钥调度算法,反推初始秘钥,或者继续爆破
所以,我们怎么办,如何设计S盒?
- 去掉S盒?
-
答:这肯定是不行的,S盒为整个分组密码的非线性部(这并不妨碍S盒有线性特征),去掉之后输入明文和输出的密文就会存在非常明显的位置对应关系。
- 让S盒的所有异或表达式的概率全为0.5?
- 这在数学上是做不到的,但是可以让表达式更平均,比如AES的S盒生成算法。